Đề cương ôn tập học kỳ II môn Toán Lớp 11 - Năm học 2019-2020 - Trường THPT Nguyễn Trung Trực

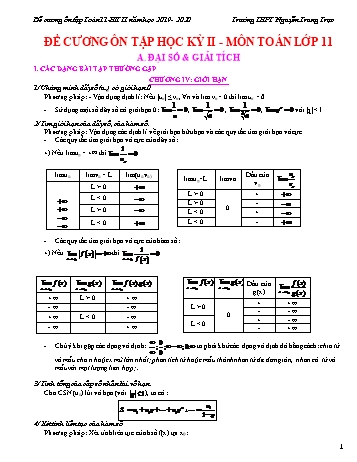
n giản, nhân cả tử và mẫu với một lượng liên hợp;
3/ Tính tổng của cấp số nhân lùi vô hạn
Cho CSN (un) lùi vô hạn (với ), ta có : 
4/ Xét tính liên tục của hàm số
Phương pháp: Xét tính liên tục của hsố f(x) tại x0:
+) Tính f(x0)
+) Tìm (nếu có)
- Nếu không tồn tạiÞ f(x) gián đoạn tại x0.
- Nếu Þ f(x) gián đoạn tại x0
- Nếu Þ f(x) liên tục tại x0.
5/ Chứng minh sự tồn tại nghiệm của một phương trình.
Phương pháp: Vận dụng hệ quả của định lí về giá trị trung gian: Nếu hàm số y = f(x) liên tục trên đoạn [a;b] và f(a).f(b) < 0 thì phương trình f(x) = 0 có ít nhất 1 nghiệm nằm trong (a ; b).
CHƯƠNG V: ĐẠO HÀM
1/ Tìm đạo hàm của hàm số
Phương pháp: Áp dụng các công thức tính đạo hàm
+) Các quy tắc tính đạo hàm:
+) Đạo hàm của hàm hợp: Nếu thì 
+) Đạo hàm của các hàm số lượng giác: 
2/ Viết phương trình tiếp tuyến của đồ thị hàm số.
Phương pháp:pt tiếp tuyến của đồ thị hàm số y = f(x) tại điểm M0 có hoành độ x0 có dạng:
	 y = f’(x0) (x – x0) + f(x0)
3/ Vi phân
- Vi ph...biết rằng:
a) f(x) = cos x + sin x + x.	b) f(x) = 	
c) f(x) = 3cosx + 4sinx + 5x	d) f(x) = 2x4 – 2x3 – 1 
Bài 6: Cho hàm số 
Bài 7: a) Cho hàm số: . Chứng minh rằng: 2y.y’’ – 1 =y’2
b) Cho hàm số y = . Chứng minh rằng: 2(y’)2 =(y -1)y’’
c) Cho hàm số . Chứng minh rằng:
d) Cho hàm số . Chứng minh : .
Bài 8: 
 1. Cho hàm số: . Giải phương trình: y’ = 0
 2. Cho hàm số: . Giải phương trình: y’ = 0 
 3 Cho hàm số: . Giải phương trình: y’ = 0
Bài 9: Chứng minh rằng , biết:
a/ b/ 
Bài 10:. Cho hàm số : y = x4 + 2x2 – 1 . Viết phương trình tiếp tuyến của (C) trong mỗi trường hợp sau
Tiếp điểm M(-1;2).
Biết rằng tiếp điểm bằng 2.
Biết rằng tiếp tuyến song song với trục hoành.
Biết rằng tiếp tuyến vuông góc với đường thẳng .
Biết rằng tiếp tuyến đi qua điểm A(0;6).
Bài 11: Cho đường cong . Viết phương trình tiếp tuyến của trong các trường hợp sau :
a) Tại điểm .
b) Tại điểm thuộc và có hoành độ .
c) Tại giao điểm của với trục hoành . 
d) Tiếp tuyến song song với đường thẳng d: y = 9x + 2.
d) Biết tiếp tuyến đi qua điểm.
Bài 12: Gọi ( C) là đồ thị hàm số : . Viết phương trình tiếp tuyến của (C ) 
a) Tại M (0;2).
b) Biết tiếp tuyến có hệ số góc là -3.
c) Biết tiếp tuyến vuông góc với đường thẳng y =x – 4.
Bài 13: Cho đường cong (C): . Viết phương trình tiếp tuyến của đồ thị (C)
a) Tại điểm có hoành độ bằng 1.	
b) Tại điểm có tung độ bằng .
c) Biết tiếp tuyến đó có hệ số góc là .
d) Biết tiếp tuyến song song với đt 16x + y - 5 =0 .
Bài 14: Cho đường cong . Viết phương trình tiếp tuyến của 
a) Biết tiếp tuyến song song với đường thẳng .
b) Biết tiếp tuyến vuông góc với đường thẳng .
c) Viết p trình tiếp tuyến của biết tiếp tuyến tạo với đường thẳng d : một góc .
Bài 15: Cho hàm số . Viết phương trình tiếp tuyến của đồ thị hàm số (1), biết tiếp tuyến đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác OAB cân tại gốc tọa độ O.
Bài 16: Cho hàm số . Tìm các điểm thuộc đồ thị mà qua đó kẻ được một và chỉ một tiếp tuyến...nh chiếu H của A lên b
AH là đoạn vuông góc chung của a và b
+) Phương pháp 2: 
Dựng (P) É a và (P) // b.
Dựng hình chiếu b’ của b lên (P). b’ // b, b’ Ç a = H
Dựng đt vuông góc với (P) tại H cắt đt b tại A.
AH là đoạn vuông góc chung của a và b.
+) Phương pháp 2: 
Dựng đt (P) ^ a tại I cắt b tại O
Xác định hình chiếu b’ của b trên (P) (b’ đi qua O).
Kẻ IK ^ b’ tại K.
Dựng đt vuông góc với (P) tại K, cắt b tại H.
Kẻ đt đi qua H và song song với IK, cắt đt a tại A.
AH là đoạn vuông góc chung của a và b.
II. BÀI TẬP
Bài 1: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B. SA ^ (ABC).
Chứng minh: BC ^ (SAB).
Gọi AH là đường cao của DSAB. Chứng minh: AH ^ SC.
Bài 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông. SA ^ (ABCD). Chứng minh rằng:
BC ^ (SAB).
SD ^ DC.
SC ^ BD.
Bài 3: Cho tứ diện ABCD có AB=AC, DB=DC. Gọi I là trung điểm của BC.
Chứng minh: BC ^ AD.
Gọi AH là đường cao của DADI. Chứng minh: AH ^ (BCD).
Bài 4: Cho hình chóp S.ABCD có đáy là hình vuông, tâm O và SA = SC = SB = SD = . 
Chứng minh SO ^ (ABCD).
Gọi I, K lần lượt là trung điểm của AB và BC. Chứng minh IK^SD
Tính góc giữa đt SB và mp(ABCD).
Bài 5: Cho tứ diện ABCD có AB ^ CD, BC ^ AD. Gọi H là hình chiếu của A lên mp(BCD). Ch. minh:
H là trực tâm DBCD.	b) AC ^ BD.
Bài 6: Cho tứ diện đều ABCD. Chứng minh rằng các cặp cạnh đối diện của tứ diện vuông góc với nhau từng đôi một.
Bài 7: Cho hình chóp S.ABCD có đáy là HCN, tâm O và AB = SA = a, BC = , SA ^ (ABCD).
Chứng minh các mặt bên của hình chóp là những tam giác vuông.
Gọi I là trung điểm của SC. Chứng minh IO^ (ABCD).
Tính góc giữa SC và (ABCD).
Bài 8: Cho hình chóp S.ABCD có đáy là hình vuông, tâm O và SA (ABCD) . Gọi H, K lần lượt là hình chiếu vuông góc của A lên SB, SD.
Chứng minh BC ^ (SAB), BD ^ (SAC).	b) Chứng minh SC ^ (AHK).
c) Chứng minh HK ^ (SAC).
Bài 9: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, SA = AB = AC = a, SA ^ (ABC).
Gọi I là trung điểm BC.
a) Chứng minh BC ^ (SAI). 	b)