Đề thi thử THPT Quốc gia năm 2020 môn Toán - Trường THCS&THPT Trần Văn Lâm (Có đáp án)

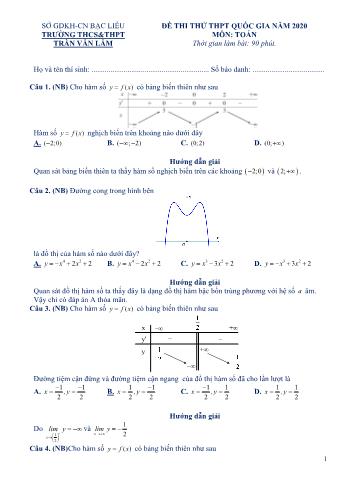
x , y
 C. 
1 1
2 2
x , y
 D. 
1 1
2 2
x , y 
Hướng dẫn giải 
Do 
1
2
x
lim y
 và 
1
2x
lim y
Câu 4. (NB)Cho hàm số ( )y f x có bảng biến thiên như sau 
x 
y 
y 
– 
– – 
+ 
– 
+ 
2 
Hàm số đạt cực đại tại điểm 
A. 1x B. 0x C. 5x D. 2x 
Hướng dẫn giải 
Quan sát bảng biến thiên ta thấy hàm số đạt tiểu tại điểm 0x và đạt cực đại tại điểm 2x . 
Câu 5. (TH)Đồ thị của hàm số nào dưới đây có tiệm cận đứng 
A. 
2 3 2
1
x x
y
x
 B. 
2
2 1
x
y
x
 C. 
2 1y x D. 
1
x
y
x
Hướng dẫn giải 
 2 2 13 2
2
1 1
x xx x
y x
x x
 đồ thị hàm số không có tiệm cận đứng. 
2
2 1
x
y
x
 có: 2 1 0x x R  đồ thị hàm số không có tiệm cận đứng. 
2 1y x không có tiệm cận đứng. 
1
x
y
x
 Có 
1
lim 1
1x
x
x
x 
 là tiệm cận đứng của đồ thị hàm số. 
Câu 6. (TH)Cho hàm số ( )y f x có bảng biến thiên như sau 
Số nghiệm phương trình 3 ( ) 2 0f x là 
A. 0 B. 3 C. 1 D. 2 
Hướng dẫn giải 
Số nghiệm của phương trình 
2
3 2 0
3
f x f x là số giao... đó 
1 1 6
; . . . 24 6 3
2 2 2
ABCS d C AB AB . 
Câu 12.(VDC) Cho hàm số y f x liên tục trên có đồ thị như hình vẽ. Biết trên 
 ; 3 2;  thì 0f x . 
Số nghiệm nguyên thuộc 10;10 của bất phương trình 2 3 26 2 5 6f x x x x x x là 
A. 9 B.
10 C. 8 D. 7 
Hướng dẫn giải 
Ta có 2 3 2 26 2 5 6 1 6 0f x x x x x x f x x x x 
5 
+ Trường hợp 1 : 
2 6 0 2 3
3 2 3
3 1 21 0
x x x x
x x
x xf x x
  
  
  
+ Trường hợp 2 : 
2 6 0 2 3
1 2
3 1 21 0
x x x
x
x xf x x
  
+ Từ hai trường hợp trên ta được các nghiệm nguyên thuộc 10;10 là 
 0;1;4;5;6;7;8;9 . 
Câu 13. (NB) Cho ,x y là hai số thực dương và ,m n là hai số thực tùy ý. Đẳng thức nào sau đây 
là sai? 
A. .m n m nx x x B.
 .
n n nxy x y C. 
m
n nmx x D. .
m nm nx y xy
Câu 14. (NB) Số thực a thỏa điều kiện 3 2log (log ) 0a là: 
A. 
1
3
 B.
3 C. 
1
2
 D. 2 
Hướng dẫn giải 
3 2 2log (log ) 0 log 1 2a a a 
Câu 15. (TH) Với giá trị nào của x thì biểu thức 2( ) log (2 1)f x x xác định? 
A. 
1
;
2
x
 B.
1
;
2
x
 C. 
1
\
2
x
 
 
 
 D. x ( 1; ) 
Hướng dẫn giải 
 2
( ) log (2 1)f x x xác định khi 
1
2 1 0
2
x x 
Câu 16. (TH) Đạo hàm của hàm số 3 .x xy e 
A. 
1
. 3
x
x e
 B.
 3 . ln 3x xe e C. 3 . ln3 ln1
x xe D. 3 . ln 3 1x xe 
Hướng dẫn giải 
/
/ 3 . 3 . ln 3 3 . ln3 1x x x x x xy e e e e 
Câu 17. (TH) Phương trình 9 5.3 6 0x x có tổng các nghiệm là: 
A. 3log 6 B.
3
2
log
3
 C. 3
3
log
2
 D. 3log 6 
Hướng dẫn giải 
3log 23 2
9 5.3 6 0
13 3
x
x x
x
x
x
tổng các nghiệm là 
3 3 3 3log 2 1 log 2 log 3 log 6 
Câu18.(VD) Tìm tất cả các giá trị thực của tham số m để phương trình 
 23 3log 2 log 3 1 0x m x m có hai nghiệm 1 2,x x thỏa mãn 1 2. 27.x x ? 
A. 2m B.
1m C. 1m D. 2m 
6 
Hướng dẫn giải 
Điều kiện 0.x Đặt 3log .t x Khi đó phương trình có dạng: 
2 2 3 1 0t m t m . 
Để phương trình có hai nghiệm phân biệt thì 
2 2
4 2 2
2 4 3 1 8 8 0 *
4 2 2
m
m m m m
m
Với điều kiện * ta có: 1 2 3 1 3 2 3 1 2 3log log l... e e dx x e e dx 
Câu26.(VDC) Cho hàm số y f x liên tục trên R và thỏa mãn 2018 sin .f x f x x x
Tính tích phân 
2
2
?I f x dx 
8 
A. 
1
.
2020
I B.
2
.
2019
I C. 
1
.
2019
I D. 
1
.
2018
I 
Hướng dẫn giải 
2018 sin . 2018 sin .f x f x x x f x f x x x 
2 12018 1 2017 sin sin
2019
f x x x f x x x 
2 2
2
2
2 2
1 1 1 2
sin cos sin
2019 2019 2019 2019
I x xdx xd x x
Câu27.(NB) Cho số phức 3 4z i . Khẳng định nào sau đây là khẳng định sai? 
A. Điểm biểu diễn của z là 4;3M . B.
Môđun của số phức z là 5. 
C. Số phức đối của z là 3 4i . D. Số phức liên hợp của z là 3 4i . 
Hướng dẫn giải 
z có phần thực bằng 3,phần ảo bằng 4 nên điểm biểu diễn của z là 3;4M 
Câu28.(TH) Cho số phức 
2
3 2 1z i i . Môđun của w iz z là 
A. 2. B.
2 2 . C. 1. D. 2 . 
Hướng dẫn giải 
* 
 2 4 6 6 4
3 2 1 3 2 2 4 6
4 6
iz i i i
z i i i i i
z i
* 6 4 4 6 2 2w iz z i i i 
2 2
2 2 8 2 2w 
Câu29.(TH) Cho số phức z thỏa mãn điều kiện: 1 1 3 0i z i . Phần ảo của số phức 
1w iz z là 
A. 1 B.
3 . C. 2 . D. 1 . 
Hướng dẫn giải 
1 1 3 0
1 3 11 3 4 2
2 2
1 1 1 2
1 1 2 2 2 3
i z i
i ii i
z i z i
i i i
w iz z i i i i
Phần ảo của w là 3 
Câu30.(VD) Cho phương trình 2 6 0z mz i . Để phương trình có tổng bình phương hai 
nghiệm bằng 5 thì m có dạng ,m a bi a b . Giá trị 2a b là: 
A. 1 B.
0 . C. 2 . D. 1 . 
Hướng dẫn giải: 
Gọi 1 2,z z là hai nghiệm của phương trình đã cho 
Theo Viet, ta có: 
1 2
1 2. 6
b
S z z m
a
c
P z z i
a
Theo bài cho, tổng bình phương hai nghiệm bằng 5. Ta có: 
9 
22 2 2 2 2 2
1 2 2 12 5 5 12 3 2
3 2
z z S P m i m i m i
m i
3; 2 2 3 4 1a b a b 
Câu31.(VDC) Cho hai số phức 1z và 2z thỏa mãn 1 3z , 2 4z , 1 2 37z z . Xét số phức 
1
2
z
z a bi
z
 . Tìm b . 
A. 
3 3
8
b B.
39
8
b . C. 
3
8
b . D. 
3
8
b . 
Hướng dẫn giải 
Đặt 1z x yi , 2z c di , , ,x y c d . Ta có: 
2 2
1 3 9z x y ; 
2 2
2 4 16z c d ; 
2 2 2 2 2 2
1 2 37 37 2 2 37 6z z x c y d x y c d xc yd xc yd . 
Lại có